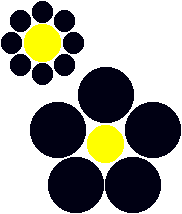
De nombreuses illusions produisent une mise en relation de grandeur des éléments de la figure. Il en résulte généralement un effet de contraste : la grandeur apparente des éléments les plus grands est surestimée par comparaison au plus petit et inversement. Le cas le plus évident est sans doute l’illusion de Titchener (ci-desosus) où le cercle central de la configuration de gauche paraît plus grand que celui de la configuration de droite : (n'oubliez pas de déplacer votre souris sur l'illusion). On a cependant invoqué à certains moments le principe d’assimilation suivant lequel, lorsque les différences sont minimes entre les plus grands et les plus petits éléments, on a tendance à minimiser ces différences. Il s’ensuit une assimilation d’un élément test à un élément inducteur plus grand (donc un surestimation de l’élément test) ou plus petit ( donc une sous-estimation de l’élément test), alors que le contraste apparaît lorsque la différence entre l’élément inducteur et l’élément test est plus importante.   

La courbure des arcs de cercle varie en fonction de leur longueur. Les arcs court sont vus plus plats que les arcs longs comme nous pouvons le remarquer sur l'illusion ci-dessous où les trois lignes semblent avoir des courbures différentes alros qu'elle ont la même la courbure.

Les illusions dues à des effets d’angles sont très nombreuses et elles sont sans doute parmi les plus spectaculaires. Les scientifiques se sont appuyés sur deux principes pour les expliquer.
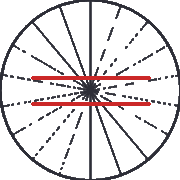
Tout d'abord, nous avons tendance à sur-estimer les angles aigus et a sous-estimer les angles obtus. Nous avons qualifié ceci de principe d’orthogonalité, étant donné qu’il s’agit dans chaque cas d’une tendance à ramener l’angle vers un angle droit. Ce principe permet d’expliquer facilement les illusions de Zöllner (ci-dessous, à droite) où les lignes obliques ne semblent pas parallèles, alors qu’elles le sont et de Hering (ci-dessous, à gauche) où les deuxsegments rouges semblent incurvées, alors qu’elles sont physiquement droites et parallèles., mais il peut aussi s’appliquer à l’illusion de Poggendorff et à celle de Müller-Lyer (page 1). Dans l'illusion de Zöllner, les lignes nous paraissent déformées à cause des petites lignes qui forment le graphisme secondaire.

Le second principe concerne la tendance que l’on a à sur-estimer les côtés d’un angle obtus et à sous-estimer ceux d’un angle aigu. Dans ce cas, l’illusion de Müller-Lyer pourrait encore servir d’exemple.

1.2.3.4.5