Cette expérience nous permet de simuler le trajet de la lumière d'un mirage sous la forme d'un graphique.

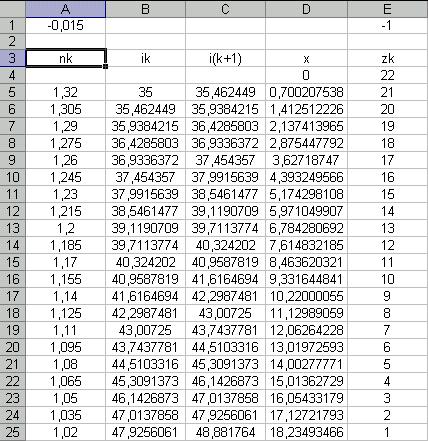
• Remplire un tableur excell à cinq colonnes de la facon suivante.
        n (k) étant l'indice de l'air; il varie de delta n a chaque milieu: n (k+1)=                      n(k)+delta n

        i(k) et i(k+1) sont les angles d'incidences, on trouve leur valeur avec la loi de                 Descartes n(1)sin(i1) = n(2)sin(i2)

        x est la distance horiontale, c'est a dire que x(k+1) = x(k)+tan(ik)*(delta z)      

        zk est l'altitude: elle diminue d'un metre a chaque indice

• On obtient alors les valeurs suivantes:

Exploitation:
• En faisant varier l'angle d'incidence initiale ou delta n on peut creer differents graphiques simulant un mirage.
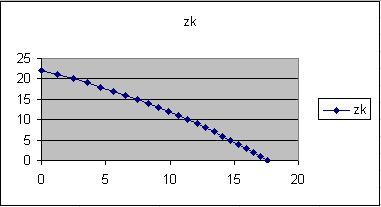
• On cree d'abord un grphique donnant z(k) en fonction de x.
Pour les valeurs initiale que l'on a choisie, on obtient le graphique suivant:

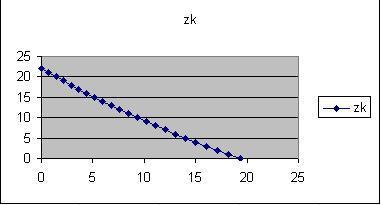
On constate que le rayon atteind le sol en s'incurvant vers le bas, comme dans un mirage inférieur.

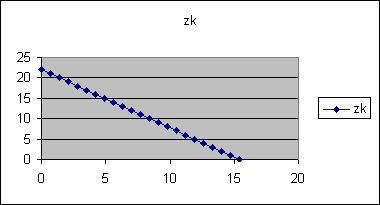
• Si on prend delta n nul, on simule un milieu homogène. Le rayon n'est alors pas diffracté: il se propage en ligne droite.

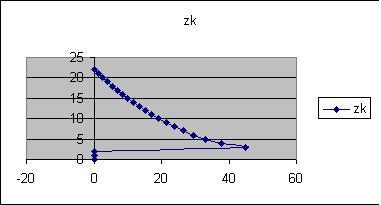
• Si on prend un angle initial de 52° (en concervant delta(n)=-0,015) le tableur affiche une impossibilité à partir d'une certaine valeur et la courbe est défomée. C'est parce qu'il y a une réfléxion total au point (45;3).

• Et si on prend delta(n)=0,04 avec un angle initial de 52°, le rayon s'incurve vers le haut (régions de plus grand indice) comme dans le cas d'un mirage supérieur.

Voici le fichier que nous avons fait sur excel, pour ceux qui des difficultés à le recréer à partir des explications et des images ci-dessus, vous pouvez le télécharger en cliquant sur le lien : mirages excel

page précédente

PAGE SUIVANTE